Resistive Circuits

Thévenin’s Theorem – Circuit with Two Independent Sources

Use Thévenin’s theorem to determine $I_O$ .

Thevenin's Theorem - Circuit containing two independent sources

Fig. (1-27-1) - Circuit with two independent sources

Solution
Lets break the circuit at the $3\Omega$ load as shown in Fig. (1-27-2).

Fig. (1-27-2) - Breaking circuit at the load

Now, we should find an equivalent circuit that contains only an independent voltage source in series with a resistor, as shown in Fig. (1-27-3).

Fig. (1-27-3) - The Thevenin equivalent circuit

Unknowns are $V_{Th}$ and $R_{Th}$ . $V_{Th}$ is the open circuit voltage $V_{OC}$ shown in Fig. (1-27-2).
It is trivial that the current of $2\Omega$ resistor is equal to the current of the current source, i.e. $I_{2\Omega}=-1A$ . Therefore, $V_{OC}=V_{2\Omega}=2\Omega \times I_{2\Omega}=-2V$ . The Thévenin theorem says that $V_{Th}=V_{OC}=-2V$ . Please note that it is not saying that $V_{OC}$ is the voltage across the load in the original circuit (Fig. (1-27-1)). To find the other unknown, $R_{Th}$ , we turn off independent sources and find the equivalent resistance seen from the port, as this is an easy way to find $R_{Th}$ for circuits without dependent sources. Recall that in turning independent sources off, voltage sources should be replace with short circuits and current sources with open circuits. By turning sources off, we reach at the circuit shown in Fig. (1-27-4).

Fig. (1-27-4) - Turning off the sources to find Rth

The $6\Omega$ resistor is short circuited and the $5\Omega$ one is open. Therefore, their currents are zero and $R_{Th}=2\Omega$ .
Now that we have found $V_{Th}$ and $R_{Th}$ , we can calculate $I_O$ in the original circuit shown in Fig. (1-27-1) using the Thévenin equivalent circuit depicted in Fig. (1-27-3). It is trivial that
$I_{O}=\frac{V_{th}}{R_{Th}+3 \Omega}=\frac{-2V}{2\Omega+3 \Omega}=-\frac{2}{5}A$ .
We used the Thévenin Theorem to solve this circuit. A much more easier way to find $I_O$ here is to use the current devision rule. The current of the current source is divided between $2\Omega$ and $3\Omega$ resistors. Therefore,
$I_{O}=\frac{2\Omega}{2\Omega+3 \Omega} \times (-1A)=-\frac{2}{5}A$
Now, replace the current source with a $-1V$ voltage source as shown below and solve the problem. The answers are $V_{th}=\frac{4}{7} V$ , $R_{th}=\frac{10}{7}\Omega$ and $I_O=\frac{4}{31}A$ . Please let me know how it goes and leave me a comment if you need help

Fig (1-27-5) - Homework

Thévenin’s Theorem – Circuit with An Independent Source

Use Thévenin’s theorem to determine $V_O$ .

Fig. (1-26-1) - The Circuit

Solution
To find the Thévenin equivalent, we break the circuit at the $4\Omega$ load as shown below.

Fig. (1-26-2) - Breaking the circuit at the load

So, our goal is to find an equivalent circuit that contains only an independent voltage source in series with a resistor, as shown in Fig. (1-26-3), in such a way that the current-voltage relationship at the load is not changed.

Fig. (1-26-3) - Replacing the Thevenin equivalent circuit

Now, we need to find $V_{Th}$ and $R_{Th}$ . $V_{Th}$ is equal to the open circuit voltage $V_{OC}$ shown in Fig. (1-26-2). The current of $2\Omega$ resistor is zero because one of its terminals is not connected to any element; therefore, current cannot pass through it. Since the current of $2\Omega$ resistor is zero, the $9V$ voltage source, $3\Omega$ and $6\Omega$ resistors form a voltage divider circuit and the voltage across the $6\Omega$ resistor can be determined by the voltage devision rule. Please not that we are able to use the voltage devision rule here just because the current of the $2\Omega$ resistor is zero. You may ask that there is no reason to prove that the current of the $2\Omega$ resistor is zero in the original circuit shown in Fig. (1-26-1). That is correct. However, we are calculating $V_{OC}$ for the circuit shown in Fig. (1-26-1) and this is a different circuit. The Thévenin theorem guarantees that $V_{Th}=V_{OC}$ , it is not saying that $V_{OC}$ is the voltage across the load in the original circuit.
$V_{6\Omega}=\frac{6\Omega}{3\Omega+6\Omega}\times 9 V= 6V$
Since the current of the $2\Omega$ resistor is zero:
$V_{OC}=V_{6\Omega}=6V$
$V_{Th}=V_{OC}=6V$
Now, we need to find $R_{Th}$ . An easy way to find $R_{Th}$ for circuits without dependent sources is to turn off independent sources and find the equivalent resistance seen from the port. Recall that voltage sources should be replace with short circuits and current sources with open circuits. Here, there is only a voltage source that should be replaced by short circuit as shown in Fig. (1-26-4).

Fig. (1-26-4) - Turning off the voltage source to find Rth

It is trivial to see that the $3 \Omega$ and $6 \Omega$ resistors are connected in parallel and then wired in series to the $2\Omega$ resistor. Therefore,
$R_{Th}=(3\Omega || 6\Omega)+2\Omega=\frac{3\Omega \times 6\Omega}{3\Omega + 6\Omega}+2\Omega=4\Omega$ .
Now that $V_{Th}$ and $R_{Th}$ are found, we can use the Thévenin equivalent circuit depicted in Fig. (1-26-3) to calculate $V_O$ in the original circuit shown in Fig. (1-26-1). The voltage devision rule can be used here to find $V_O$ . We have,
$V_{O}=\frac{4\Omega}{R_{Th}+4 \Omega}\times V_{Th}=\frac{4\Omega}{4\Omega+4 \Omega}\times 6V=3V$ .

Superposition Method – Circuit With Dependent Sources

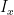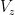Determine $I_x$ , $I_y$ and $V_z$ using the superposition method.

Superposition - Circuit with dependent sources

Solution
I. Contribution of the $-2V$ voltage source:
We need to turn off the current source by replacing it with an open circuit. Recall that we do not turn off dependent sources. The resulting circuit is shown below.
Superposition - Circuit with dependent sources - Contribution of the -2V voltage source

Superposition - Circuit with dependent sources - Contribution of the -2V voltage source

In the left hand side loop, we have
$6I_{x1}=1 \Omega \times I_{y1}$
and in the right hand loop, it is trivial that
$2I_{y1}=I_{x1}$ .
Therefore, $I_{x1}=I_{y1}=0$ . Applying KVL around the inner loop,
$-V_{z1}-1\Omega\times I_{y1}+(-2V)-2\Omega \times I_{x1}=0$
Substituting $I_{x1}=I_{y1}=0$ , we have
$V_{z1}=-2V$ .
II. Contribution of the $11A$ current source:
The independent voltage source must be replaced with a short circuit as shown below.
Superposition - Circuit with dependent sources - Contribution of the 11A current source

Superposition - Circuit with dependent sources - Contribution of the 11A current source

The $1\Omega$ resistor is parallel with the dependent voltage source, Therefore, $V_{1\Omega}=6I_{x2}$ and since $V_{1\Omega}=1\Omega \times I_{y2}$ , we have $6I_{x2}=I_{y2}$ . Applying KCL at the right bottom node, $11A-I_{x2}+2I_{y2}$ . So,
$\left\{ \begin{array}{l} 6I_{x2}=I_{y2} \\ I_{x2}-2I_{y2}=11 \end{array} \right. \to \left\{ \begin{array}{l} I_{x2}=-1 A \\ I_{y2}=-6A \end{array} \right.$
Applying KVL around the inner loop,
$+2\Omega \times I_{x2}+1 \Omega \times I_{y2}+V_{z2}=0 \to V_{z2}=8V.$

III. The final result
$I_x=I_{x1}+I_{x2}=-1 A$
$I_y=I_{y1}+I_{y2}=-6 A$

$V_z=V_{z1}+V_{z2}=6V$

Superposition Problem with Four Voltage and Current Sources

Determine $V_x$ and $I_x$ using the superposition method.
A circuit with four voltage and current sources to be solved by the superposition method

Solution
I. Contribution of the $-5V$ voltage source:
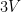To find the contribution of the $-5V$ voltage source, other three sources should be turned off. The $3V$ voltage source should be replaced by short circuit. The current source should be replaced with open circuits, as shown below.
Superposition - Finding the contribution of the -5V voltage source

Superposition - Finding the contribution of the -5V voltage source

It is trivial that $I_{x1}= \frac{-5 V}{2 \Omega}=-2.5 A$ . The current of the $3\Omega$ resistor is zero. Using KVL, $-(-5V)+V_{3\Omega}-V_{x1}=0 \to V_{x1}=-(-5V)=5V$ .
II. Contribution of the $3V$ voltage source:
Similarly, the $-5V$ voltage source becomes a short circuit and the current source should be replaced with open circuits:
Superposition - Contribution of the 3V voltage source

Superposition - Contribution of the 3V voltage source

The current of the $2\Omega$ resistor is zero because of being short circuited. It is trivial that $I_{x2}= 0 A$ (current of an open circuit). The current of the $3\Omega$ resistor is also zero. Using KVL, $-(3V)+V_{2\Omega}+V_{x2}+V_{3\Omega}=0 \to V_{x2}=3V$ .
III. Contribution of the $-1A$ current source:
The voltage sources should be replaced by short circuits and the $2A$ current source becomes with open circuit:

Superposition - Contribution of the -1A current source

Again, the $2\Omega$ resistor is short circuited and its current is zero. it is clear that $I_{x3}= 1 A$ . The current of the $3\Omega$ resistor is equal to $-1A$ . Using KVL, $V_{x3}+V_{3\Omega}=0 \to V_{x3}+(-1A)\times (3\Omega)=0 \to V_{x3}=3V$ .
IV. Contribution of the $2A$ current source:
Likewise, the voltage sources should be replaced by short circuits and the $-1A$ current source becomes with open circuit:
Superposition - Contribution of the 2 A current source

Superposition - Contribution of the 2 A current source

Again, the $2\Omega$ resistor is short circuited and its current is zero. it is also trivial that $I_{x4}= 0A$ . The current of the $3\Omega$ resistor is $2A$ . Using KVL, $V_{x4}+V_{3\Omega}=0 \to V_{x4}+(2A)\times (3\Omega)=0 \to V_{x4}=-6V$ .
V. Adding up the individual contributions algebraically:
$V_x=V_{x1}+V_{x2}+V_{x3}+V_{x4}=5V+3V+3V-6V\to V_x=5V$

$I_x=I_{x1}+I_{x2}+I_{x3}+I_{x4}=-2.5A+1A+0A-0A\to I_x=-1.5A$

Nodal Analysis Problem with Dependent Voltage and Current Sources

Solve the circuit with the nodal analysis and determine $i_x$ and $V_y$ .
nodal analysis problem with dependent voltage and current sources

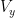Solution
1) Identify all nodes in the circuit. Call the number of nodes $N$ .
The circuit has 5 nodes. Therefore, $N=5$ .
Nodes

2) Select a reference node. Label it with reference (ground) symbol.
The node at the bottom is the best candidate. It is the node with largest number of elements connected to it.
The reference node

3) Assign a variable for each node whose voltage is unknown.
Four nodes are remaining:
non-reference nodes

Node I is a regular node. A dependent voltage source is located between node II and node III. Therefore, node II and node III form a supernode. Node IV is connected to a voltage source whose other node is the reference node. We label the voltages of node I and node II with $V_1$ and $V_2$ respectively.
Labelling nodes

For node IV, the $2V$ voltage source provides the voltage of the node. Since the positive terminal of the voltage source is connected to the node, the node voltage is $2 V$ .
A voltage source between a node and the reference node

A voltage source between a node and the reference node

4) If there are dependent sources in the circuit, write down equations that express their values in terms of other node voltages.
The voltage of node III is $V_2+3i_x$ . On the other hand $i_x$ is the current of the $2 \Omega$ resistor in the right hand side. Using the Ohm’s law:
voltage of the $2 \Omega$ resistor = $V_2+3i_x= -2 i_x$ . (Eq. 1)
Please note that the direction of $i_x$ is from the reference node to node III. Since it is always assumed that the reference node is the negative terminal for the defined node voltages, the voltage of node III is $-2 \times i_x$ (instead of $2 \times i_x$ ).
By solving Eq. 1:
$V_2= -5 i_x$ .
Consequently, the voltage of node III is $V_2+3i_x=V_2-\frac{3}{5}V_2=0.4 V_2$ .
Note that we always write unknowns in terms of node voltages in nodal analysis.
Labelled node voltages

Note that $V_2 \neq 2V_y$ . $2V_y$ is the current of the dependent current source. Now, we need to find the current of the dependent current source in terms of the node voltages. $V_y$ is the voltage across node IV and Node I. The positive terminal is connected to node IV and the negative one is connected to node II. Therefore, $V_y=2-V_1$ . You can verify this by applying KVL around the loop consisting of the reference node, node I and node IV.
5) Write down a KCL equation for each node by setting the total current flowing out of the node to zero.
For node I:
$9A + \frac{V_1 - V_2}{1 \Omega}+\frac{V_1 - 2 V}{2 \Omega}=0$ .
$\to - \frac{3}{2} V_1 +V_2=8$ (Eq. 2)
For supernode II&III:

$-2V_y+\frac{V_2-V_1}{1 \Omega}+\frac{0.4V_2}{2 \Omega}+\frac{0.4V_2-2V}{1 \Omega}=0$ . Substituting $V_y=2-V_1$ and simplifying:
$- V_1 -1.6 V_2=-6$ . (Eq. 3)
Solving the set of equations Eq. 2 and Eq. 3 results in $V_1=-2 V$ and $V_2=5V$ . Therefore $V_y=2-V_1=4 V$ and $i_x=-0.2 V_2=-1 A$ .

Nodal Analysis – Circuit with Dependent Voltage Source

Determine the power of each source after solving the circuit by the nodal analysis.
Nodal Analysis - Supernode - Dependent Voltage Source 1

Answers: $P_{I_x}=0.497W, P_{1A}=-1.806W, P_{2A}=4.254W, P_{3V}=-3.87W,$ and $P_{5V}=-3.552W$

Solution
I. Identify all nodes in the circuit.
The circuit has 6 nodes as highlighted below.
Nodal Analysis - Supernode - Dependent Voltage Source - All Nodes

Nodal Analysis - Supernode - Dependent Voltage Source - All Nodes

II. Select a reference node. Label it with the reference (ground) symbol.

The right top node is connected to two voltage sources and has three elements. All other nodes also have three elements. Hence, we select the right top node because by this selection, we already know the node voltages of two other nodes, i.e. the ones that the reference node is connected to them by voltage sources.
Nodal Analysis - Supernode - Dependent Voltage Source - The reference node and node voltages

Nodal Analysis - Supernode - Dependent Voltage Source - The reference node and node voltages

III. Assign a variable for each node whose voltage is unknown.
We label the remaining nodes as shown above. Nodes of $V_3$ and $V_4$ are connected to the reference node through voltage sources. Therefore, $V_3$ and $V_4$ can be found easily by the voltages of the voltage sources. For $V_3$ , the negative terminal of the voltage source is connected to the node. Thus, $V_3$ is equal to minus the source voltage, $V_3=-5 V$ . The same argument applies to $V_4$ and $V_4=-3V$ .
IV. If there are dependent sources in the circuit, write down equations that express their values in terms of node voltages.
The voltage of the dependent voltage source is $I_x$ . We should find this value in terms of the node voltages. $I_x$ is the current of the $3\Omega$ - resistor. The voltage across the resistor is $V_2-V_4$ . We prefer to define $V_{3\Omega}$ as $V_2-V_4$ instead of $V_4-V_2$ to comply with passive sign convention. By defining $V_{3\Omega}$ as mentioned, $I_x$ is entering from the positive terminal of $V_{3\Omega}$ and we have $V_{3\Omega}= 3 \Omega \times I_x$ . Therefore, $I_x=\frac{V_2-V_4}{3\Omega}$ . $\to I_x=\frac{V_2}{3} +1$
V. Write down a KCL equation for each node.
Nodes of $V_1$ and $V_2$ :
These two nodes are connected through a voltage source. Therefore, they form a supernode and we can write the voltage of one in terms of the voltage of the other one. Please note that the voltage of the dependent voltage source is $I_x$ and we have $V_2=V_1+I_x$
$\to V_2=V_1+\frac{V_2}{3} +1 \to \frac{2}{3} V_2=V_1+1$
$\to V_1=\frac{2}{3} V_2-1$
Nodal Analysis - Supernode - Dependent Voltage Source - The supernode

Nodal Analysis - Supernode - Dependent Voltage Source - The supernode

KCL for the supernode:
$\frac{V_1-V_3}{5\Omega}+\frac{V_1-V_5}{2\Omega}+\frac{V_2-V_4}{3\Omega}-2A=0$
$\to \frac{V_1+5}{5}+\frac{V_1-V_5}{2}+\frac{V_2+3}{3}-2=0$
$\to \frac{V_1}{5}+\frac{V_1-V_5}{2}+\frac{V_2}{3}=0$
$\to 21V_1-15V_5+10V_2=0$
Substituting $V_1=\frac{2}{3} V_2-1$ ,
$\to 8V_2-5V_5=7$
Node of $V_5$ :
$\frac{V_5-V_1}{2 \Omega} +\frac{V_5-V_3}{1 \Omega}+1=0$
$\to -V_1 +3V_5-2V_3+2=0$
Substituting $V_1=\frac{2}{3} V_2-1$ and $V_3=-5 V$ ,
$\to -2 V_2 +9V_5=-39$
Here is the system of equations that we need to solve and obtain $V_2$ nd $V_5$ :
$\left\{ \begin{array}{l} I: 8V_2-5V_5=7 \\ II: -2 V_2 +9V_5=-39 \end{array} \right.$ We use elimination method to solve this system of equation:
$(II)\times 4 +(I): 31V_5=-149 \to$
$V_5=-4.806 V$
$V_2=\frac{9V_5+39}{2} \to$
$V_2=-2.127 V$
Using $V_1=\frac{2}{3} V_2-1$ ,
$V_1=-2.418 V$
All node voltages are determined. Now, the power of voltage sources can be calculated from the node voltages. For each source, we need to find the voltage across the source as well as the current flowing through it to compute the power.
$2A$ current source:
The voltage across the $2A$ current source is equal to $V_2$ . However, the comply with the passive voltage convention, the current should be entering from the positive terminal of the defined voltage as shown below. Therefore, $V_{2A}=-V_2=2.127 V$ .
$P_{2A}=2A \times V_{2A}=4.254W$ absorbing power
Nodal Analysis - Supernode - Dependent Voltage Source - Current directions and voltage polarities for sources

Nodal Analysis - Supernode - Dependent Voltage Source - Current directions and voltage polarities for sources

$1A$ current source:
To compliant with the passive sign convention, the voltage $V_{1A}$ should be defined with polarity as indicated above. We have $V_{1A}= V_5-V_4=-1.806V$ . Hence,
$P_{1A}=1A \times (-1.806 V)=-1.806W$ supplying power.
$5V$ voltage source:
$I_{5V}$ should be defined such that it enters from the positive terminal of the source in order to use the voltage of the source in power calculation. Another option is to use $V_3$ and define the current as entering from the voltage source terminal connected to the node of $V_3$ . We use the first approach here. KCL should be applied in the node of $V_3$ to determine $I_{5V}$ .
KCL @ Node of $V_3$ :
$-I_{5V}+I_{1\Omega}+I_{5\Omega}=0$
$\to I_{5V}=\frac{V_3-V_5}{1\Omega}+\frac{V_3-V_1}{5\Omega}=-0.7104A$
$P_{5V}=5V \times (-0.7104 A)= -3.552 W$ supplying power.
$3V$ voltage source:
Likewise, $I_{3V}$ should be defined as shown above to comply with the passive sign convention. We apply KCL to the reference node to find $I_{3V}$ .
KCL @ the reference node:
$I_{5V}+I_{3V}+2A=0$
$\to I_{3V}=-1.29A$
$P_{3V}=3V \times (-1.29 A)= -3.87 W$ supplying power.
The dependent source:
The voltage of the dependent source is $I_x$ and we define its current $I_{I_x}$ with the direction illustrated above. $I_{I_x}$ can be calculated by applying KCL at the node of $V_2$ . The current of the $3\Omega$ resistor is $I_x$ which is equal to $\frac{V_2}{3} +1= 0.291A$ .
KCL @ Node of $V_2$ :
$-2A+I_x+I_{I_x}=0 \to I_{I_x}=1.709A$ $P_{I_x}=I_x \times I_{I_x}=0.291 V \times 1.709 A= 0.497W$ absorbing power.
The PSpice simulation result is shown below. The PSpice schematics can be downloaded from http://www.solved-problems.com/download/1-23.zip.
Nodal Analysis - Supernode - Dependent Voltage Source - PSpice Simulation Results

Nodal Analysis - Supernode - Dependent Voltage Source - PSpice Simulation Results

Nodal Analysis – 6-Node Circuit

Determine the power of each source after solving the circuit by the nodal analysis.

Solution
I. Identify all nodes in the circuit.
The circuit has 6 nodes as indicated below.
Nodal Analysis 6 Node Circuit - all nodes

II. Select a reference node. Label it with the reference (ground) symbol.
The bottom left node is connected to 4 nodes while the other ones are connected to three or less elements. Therefore, we select it as the reference node of the circuit.

Nodal Analysis 6 Node Circuit - Node Voltages

III. Assign a variable for each node whose voltage is unknown.
We label the remaining nodes as shown above. $V_1$ is connected to the reference node through a voltage source. Therefore, it is equal to the voltage of the voltage source: $V_1=10V$ .
IV. If there are dependent sources in the circuit, write down equations that express their values in terms of node voltages.
There is no dependent voltage source here.
V. Write down a KCL equation for each node.
Nodes of $V_2$ and $V_3$ are connected by a voltage source. Therefore, they form a supernode. The negative terminal of the voltage source is connected to $V_3$ and the positive terminal is connected to $V_2$ . Thus, $V_2=V_3+2.$ This can also be verified by a KVL around the loop which starts from the reference node, jumps to the node of $V_3$ with $-V_3$ (the reference is always assumed to be the negative terminal of node voltages), passes through the voltage source by $-2V$ and returns back to the reference node from $V_2$ as $+V_2$ $-V_3-2V+V_2=0 \to V_2=V_3+2.$
Supernode of $V_2$ & $V_3$ :
$\frac{V_3}{1\Omega}+\frac{V_3-V_4}{5\Omega}+\frac{V_2-V_1}{2\Omega}+\frac{V_2-V_5}{3\Omega}=0$
$\to {V_3}+\frac{V_3}{5}-\frac{V_4}{5}+\frac{V_3+2-10}{2}+\frac{V_3+2-V_5}{3}=0$
$\to {V_3}+\frac{V_3}{5}-\frac{V_4}{5}+\frac{V_3}{2}-4+\frac{V_3}{3}+\frac{2}{3}-\frac{V_5}{3}=0$
$\to \frac{61}{30}V_3-\frac{V_4}{5}-\frac{V_5}{3}=\frac{10}{3}$
$\to 61 V_3-6 V_4-10 V_5=100$
Node of $V_4$ :
$\frac{V_4}{6\Omega}+\frac{V_4-V_3}{5\Omega}+10=0$
$\to 5 V_4+6 V_4-6V_3+300=0$
$\to -6V_3+11 V_4=-300$
Node of $V_5$ :
$\frac{V_5}{4\Omega}+\frac{V_5-V_2}{3\Omega}-10=0$
$\to 3V_5+4V_5-4V_2-120=0$
$\to 7V_5-4 V_3-8-120=0$
$\to -4 V_3+7V_5=128$
Hence, we have the following system of equations:
$\left\{ \begin{array}{l} 61 V_3-6 V_4-10 V_5=100 \\ -6V_3+11 V_4=-300 \\ -4 V_3+7V_5=128 \end{array} \right.$ This system of equations can be solved by any preferred method such as elimination, row reduction, Cramer’s rule or other methods. We use the Cramer’s rule here:
$V_3=\frac{ \left| \begin{array}{c c c} 100 & -6 & -10 \\ -300 & 11 & 0 \\ 128 & 0 & 7 \end{array} \right| }{ \left| \begin{array}{c c c} 61 & -6 & -10 \\ -6 & 11 & 0 \\ -4 & 0 & 7 \end{array} \right| }=\frac{9180}{4005}=2.292 V$ $V_4=\frac{ \left| \begin{array}{c c c} 61 & 100 & -10 \\ -6 & -300 & 0 \\ -4 & 128 & 7 \end{array} \right| }{ \left| \begin{array}{c c c} 61 & -6 & -10 \\ -6 & 11 & 0 \\ -4 & 0 & 7 \end{array} \right| }=\frac{-104220}{4005}=-26.022 V$ and
$V_5=\frac{ \left| \begin{array}{c c c} 61 & -6 & 100 \\ -6 & 11 & -300 \\ -4 & 0 & 128 \end{array} \right| }{ \left| \begin{array}{c c c} 61 & -6 & -10 \\ -6 & 11 & 0 \\ -4 & 0 & 7 \end{array} \right| }=\frac{78480}{4005}=19.595 V.$ Thus,
$V_2=V_3+2=4.292.$
All node voltages are found. The current of the $10 V$ source is the current of the $2\Omega$ resistor, which is $\frac{V_2-V_1}{2\Omega}=-2.854A$ The current direction shosen such that the current enters from the positive terminal of the voltage source. This is only to comply with the passive sign convention. Now that we have the source current, its power can be easily calculated:
$P_{10V}=10 \times (-2.854)=-28.54 W$ absorbing power
The current of the $2V$ source equals to the summation of the currents of $5\Omega$ and $1\Omega$ resistors. Therefore,
$I_{2V}=I_{5\Omega}+I_{1\Omega}=\frac{V_3-V_4}{5\Omega}+\frac{V_3}{1\Omega}=5.663+2.292 =7.955.$
Consequently,
$P_{2V}=2 \times 7.955=15.91W$ supplying power.
The voltage across the $10A$ current source is $V_4-V_5=-45.617$ . Therefore,
$P_{10 A}=10 \times (-45.617)=-456.17 W$ supplying power.
The PSpice simulation result is indicated below. The PSpice schematics can be downloaded from http://www.solved-problems.com/download/1-22.zip.

Nodal Analysis 6 Node Circuit - PSpice simulation result

Nodal Analysis – Dependent Voltage Source

Use nodal analysis method to solve the circuit and find the power of the 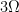$3\Omega$ - resistor.
Nodal Analysis Dependent Current Source

Solution
I. Identify all nodes in the circuit.
The circuit has 3 nodes as shown below.
Nodal Analysis Dependent Current Source - Circuit has 4 nodes

II. Select a reference node. Label it with the reference (ground) symbol.

The node in the middle is connected to 5 nodes and is the node with the largest number of elements connected to it. Therefore, we select it as the reference node of the circuit.
III. Assign a variable for each node whose voltage is unknown.
We label the remaining nodes as shown below. $V_1$ is connected to the reference node through a voltage source. Therefore, it is equal to the voltage of the dependent voltage source: $V_1=-6I_x$ .
Nodal Analysis Dependent Current Source - Reference Node - Node Voltages

Nodal Analysis Dependent Current Source - Reference Node - Node Voltages

IV. If there are dependent sources in the circuit, write down equations that express their values in terms of node voltages.
The voltage of the dependent voltage source is $-I_x$ . We should find this value in terms of the node voltages. $I_x$ is the current of the $5\Omega$ - resistor. The voltage across the resistor is $V_1-V_2$ . You may ask why not $V_2-V_1$ . Well, that is also correct; the voltage across the resistor is either $V_1-V_2$ or $V_2-V_1$ depend on which terminal we choose to be the positive one. In this circuit, we are going to use this voltage drop to determine $I_x$ . We prefer to use $V_1-V_2$ simply because $V_1$ is the voltage of the terminal that $I_x$ entering from. Therefore, the Ohm’s law can be applied in the simple form of $V=R \times I$ . By using the voltage drop $V_1-V_2$ , we have $I_x=\frac{V_1-V_2}{5\Omega}.$
V. Write down a KCL equation for each node.
Node of $V_1$ :
Because there is a voltage source in this node, there is no advantage in writing a KCL equation for this node. All we need to do is to use the voltage of the dependent voltage source and its relation with other node voltages:
$\left\{ \begin{array}{l} I_x=\frac{V_1-V_2}{5\Omega} \\ V_1=-6I_x \end{array} \right. \to V_1=\frac{6}{11}V_2.$
Node of $V_2$ :
$\frac{V_2-V_1}{5\Omega}+\frac{V_2}{3\Omega}-2A=0 \to -3V_1+8V_2=30.$
Substituting $V_1=\frac{6}{11}V_2$ ,
$V_2=\frac{33}{7} V \to V_1=\frac{18}{7} V.$
All node voltages are obtained. The power of the $3\Omega$ -resistor is
$R_{3\Omega}=\frac{V_2^2}{3\Omega}=7.408 W.$
The PSpice simulation result is illustrated below. The PSpice schematics can be downloaded from http://www.solved-problems.com/download/1-21.zip.
Nodal Analysis Dependent Current Source - PSpice simulation result

Nodal Analysis – Dependent Current Source

Deploy nodal analysis method to solve the circuit and find the power of the dependent source.
using nodal analysis method to find the power of a dependent current source

using nodal analysis method to find the power of a dependent current source

Solution
I. Identify all nodes in the circuit. Call the number of nodes $N$ .
The circuit has 4 nodes:

Therefore, $N=4$ .

II. Select a reference node. Label it with reference (ground)
symbol.
All nodes have the same number of elements. We prefer to select one of the nodes connected to the voltage source to avoid having to use a supernode.
the reference node

III. Assign a variable for each node whose voltage is unknown.
We label the remaining three nodes as shown above.
IV. If there are dependent sources in the circuit, write down equations that express their values in terms of other node voltages.
There is one dependent source, which is a current controlled current source. We need to write $-2I_1$ in terms of node voltages. $I_1$ is the current passing through the $2\Omega$ – resistor. Applying the Ohm’s law,
$I_1 = \frac{V_2-V_3}{2\Omega}$ .
Hence, $-2I_1 = V_3-V_2$ .

V. Write down a KCL equation for each node.
Node $V_1$ : $\frac{V_1}{3 \Omega}+\frac{V_1-V_2}{1\Omega}-2I_1=0$ .
$\to 4V_1-6V_2+3V_3=0$ (Eq. 1).
Node $V_2$ : $2I_1+\frac{V_2-V_1}{1\Omega}-2A+\frac{V_2-V_3}{2\Omega}=0$ .
Please note that we avoid using all unknowns except node voltages. Using $I_1$ in this KCL equation introduces an unnecessary unknown to the equations set. Substituting $2I_1 = V_2-V_3$ and rearranging results in:
$-2V_1+5V_2-3V_3=4$ (Eq. 2).
Node $V_3$ has a voltage source connected to. Therefore, $V_3=10V$ . Substituting this in Eq. 1 and Eq.2 leads to
$\left\{\begin{array}{l} 4V_1-6V_2=-30 \\ -2V_1+5V_2=34 \end{array}\right.$ .
By solving the system of equations,
$V_1=6.75V$ and $V_2=9.5$ .
Now, we need to find the voltage across the dependent current source and the current passing through it. Lets start with $I_1$ .
$I_1 = \frac{V_2-V_3}{2\Omega}=-0.25 A$ .
Assuming positive terminal placed on the node of $V_1$ , the voltage across the dependent current source is $V_1-V_2=-2.75V$ . The current flowing through the dependent current source is $-2I_1=0.5A$ . Therefore the power of the dependent current source is $-2.75 \times 0.5 = -1.375W$ . Because the current direction and the voltage polarity is in accordance with the passive sign convention and the power is negative, the dependent current source is supplying power.

Nodal Analysis – Dependent Voltage Source (5-Nodes)

Solve the circuit with the nodal analysis and determine $I_x$ .
Nodal analysis - circuit with dependent voltage source

Solution
1) Identify all nodes in the circuit. Call the number of nodes $N$ .
There are five nodes in the circuit:
Total number of nodes- Nodal Analysis

Therefore $N=5$
2) Select a reference node
The best option is the node in the bottom because it is connected to both voltage sources.
The reference node - Nodal analysis

3) Assign a variable for each node whose voltage is unknown.
There are four nodes beside the reference node:
Other nodes

Node III and Node IV are connected to the reference node through voltage sources. Therefore, their node voltages can be determined by the voltage sources.
$V_3=2I_x$ and $V_4=V_s=3V$ .

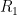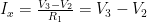$I_x$ is the current of $R_1$ . The Ohm’s law can be used to write $I_x$ in terms of the node voltages. Thus, $I_x=\frac{V_3-V_2}{R_1}=V_3-V_2$ . Substituting $V_3=2I_x$ , $I_x=2I_x-V_2 \to I_x=V_2$ (Eq. 1).
Therefore,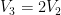 $V_3=2V_2$ .
4) Write down KCL equations.
We only need to write a KCL equation for Node I and Node II:
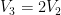Node I: $I_s + \frac{V_1-V_3}{R_2} +\frac {V_1}{R_4}=0$ . Substituting $V_3=2V_2$ and known variables,
$3V_1-2V_2=-2V$ (Eq. 2).

Node II: $-I_s+\frac{V_2-V_3}{R_1}+\frac{V2-V_4}{R_5}=0$ . $\to -1+V_2-2V_2+\frac{V_2}{2}-\frac{3}{2}=0 \to V_2=-5V$ .
Substituting in Eq. 2:
$V_1=-4V$ .
Now, we need to determine the required quantities. Eq. 1 implies that
$I_x=V_2=-4A$ .

Nodal Analysis – Supernode

Solve the circuit with nodal analysis and find 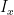$I_x$ and $V_y$ .
Nodal analysis with supernode

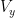Solution
1) Identify all nodes in the circuit. Call the number of nodes $N$ .
There are four nodes in the circuit:
There are four nodes in total.

Therefore $N=4$
2) Select a reference node
Because of symmetry in the circuit, any node can be chosen as the reference node.
Choosing the reference node

3) Assign a variable for each node whose voltage is unknown.
There are three nodes beside the reference node:
All nodes

Node I and Node III are connected to each other by a voltage source. Therefore, they form a supernode.

The voltage of Node III can be written in terms of the voltage of Node I. All we need to do is to apply KVL in the loop illustrated below.
Applying KVL to find the voltage of supernode

Applying KVL to find the voltage of supernode

KVL: $-V_1 -Vs_2+V_3=0 \to V_3=V_1-4$ .
A good practice is to avoid assigning a voltage label to Node III and use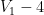 $V_1-4$ as its voltage.
Voltages of supernode - nodal analysis

There is also another voltage source which connects Node II to the reference node. This voltage source must be used to obtain the node voltage. Since the negative terminal of the voltage source is connected to the node,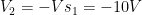 $V_2=-Vs_1=-10V$ . You can verify this by applying KVL to the loop between the reference node and Node II.
4) Write down KCL equations.
We only need to write a KCL equation for the supernode:
$-Is_2 + \frac{V_1}{R_2} +\frac {V_3 -V_2}{R_1}-Is_1=0$ . Substituting $V_3=V_1-4$ and known variables,
$V_1 =-\frac{44}{9}V$ . Therefore, $V_3 =V_1-4=-\frac{80}{9}V$

Now, we need to determine the required quantities:
KCL at node 1:
$-Is_2 +\frac{V_1}{R_2} +I_x=0 \to I_x= \frac{20}{9} A$ KVL around the loop shown in the figure below:
KVL to find Vy

$-V_3 -V_y +V_2=0\to V_y = - \frac{10}{9} v$ .

Search This Blog

Tayyab Siddiqui